交流測定の「真の実効値」型と「平均値」型

私はデジタルマルチメータをよく使いますが、そのケースに”真の実行値型”と書いてあります。実効値は何となくわかるんですが、”真の”の意味がわからずちょっと調べてみました。
せっかく調べたのでブログにまとめておきます。
まずは交流の値の定義
電圧でも電流でもいいのですが、交流の値ってどのように決まっているのでしょうか。交流の値は電圧でも電流でも”実効値”を計算して求めます。
実効値の定義は、「直流と交流を同じ抵抗にかけたときに(流したときに)同じ発熱量になる」です。
なるほど。これなら「コンセントの100VとUSBの5Vはだいたい20倍くらい違うのかー。」と想像することができますし、ほとんどの場合はこれでOKです。
実際は、コンセントの100Vは交流だし、USBの5Vは直流なので大きさを直接比較することはできません。しかし、交流か直流かを意識することなく、両方を同じ単位で比較できるように実効値が利用されるようになったんだと思います。
では、交流の実行値はどのように計算されるのでしょうか。
交流を直流に変換する方法
交流の実効値の求め方は、交流を直流に変換する方法がヒントになります。
交流の波形は(1)のようにプラスとマイナスが交互に入れ替わるような波形をしています。この電気をダイオードブリッジという電気の流れを片側に揃える素子に通すと(2)のように山型波形になります。この波形をコンデンサという波形をなめらかにする素子に通すと(3)の直流になります。

(1) (2) (3)
この方法から考えると交流の周期0から周期1/2までの波形の平均値(正弦波の場合はピークの0.707倍)が実効値になります。
2つの交流測定方法
ここまで読むと「なるほど、実効値は交流の半周期の平均値なのか!」となるんですが、残念ながらこれは正弦波のときにしか当てはまりません。
交流の振幅の平均値から実効値を計算する計測器を「平均値型」と言います。いつも正弦波を測るような装置ならこれでもいいんですが、どんな波形を測るかわからないような計測器の場合には平均値型ではなく「実効値型」や「真の実効値型」を使います。
なぜかというと、正弦波以外では数値が正しく測れないからです。例えば方形波の場合、平均値型の測定器で測ると、実際の実効値より10%ほど測定値が大きくなります。FLUKE社のサイトに良い比較があります。表のとおり平均値型は正弦波以外を正しく測れません。
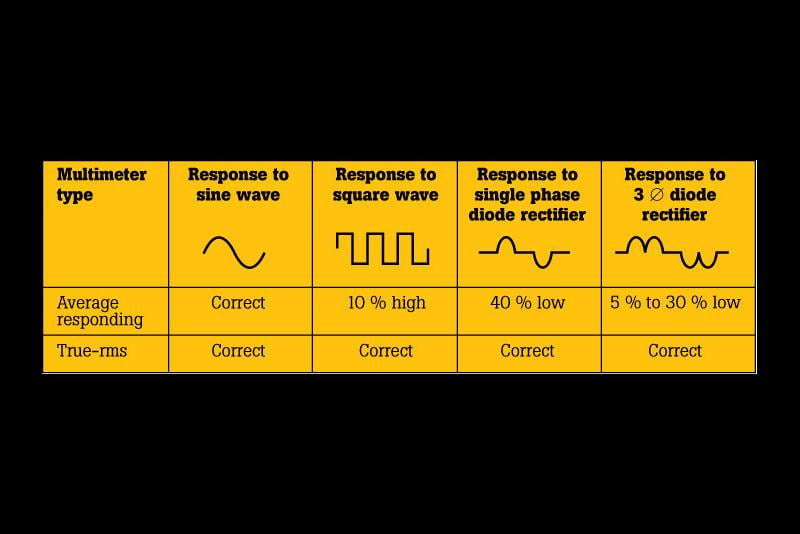
実効値型と真の実効値型は同じものです。英語表記の”True RMS(Root Mean Square)”を訳す際に”真の”がついたようです。
真の実効値型は、どう交流を測るか
真の実効値型の測定方法を考えるには、定義に戻って考えています。
交流の実効値の定義は「抵抗に電圧(電流)かけたときに同じ発熱量になる電圧(電流)値」です。発熱量なので電力で考える必要があります。
ここから先は少し数式を使います。電力\(W\)、電圧\(E\)、電流\(I\)、抵抗\(R\)の間には次のような関係があります。
$$W = EI = \frac {E^2}{R}=I^2R$$
例えば電圧の実効値の場合、交流の電力(\({E_{AC}}^2/R\))と直流の電力(\({E_{DC}}^2/R\))が等しくなるので、真の実効値を表すには自乗の平均の平方根が必要になります。周期\(N\)の交流電圧波形のデータ\(E_{AC}(n)\)の実効値\(E_{RMS}\)は次のようになります。
$$E_{RMS}=E_{DC}=\sqrt{\frac{1}{N}\sum_{n=0}^{N-1}{E_{AC}}^2(n)}$$
この式から、交流では1点の測定点から実効値を計算することができません。ですので通常はいくつかの測定点から実効値を計算しています。アジレントの高級なマルチメータだと、測定周期を入力波形の周期に同期させられる物もあります。
まとめると
まとめるとデジタルマルチメータの測定には次の2方式があります。
- 平均値型 交流波形の平均を交流の値として表示する
- (真の)実効値型 交流の定義に従って交流の実効値を表示する
実効値型で交流を測定すれば問題がないので、すべて実効値型にすればよいかもしれませんが、平均値型にも安いというメリットがあり、現在は共存状態です。
実効値と平均値のどちらかで迷ったときに、参考にしてください。
